 |
CheMPS2
|
|
CheMPS2
|
#include <EdmistonRuedenberg.h>
Public Member Functions | |
| EdmistonRuedenberg (const FourIndex *Vmat, const int group, const int printLevelIn=1) | |
| Constructor. More... | |
| virtual | ~EdmistonRuedenberg () |
| Destructor. | |
| double | Optimize (double *temp1, double *temp2, const bool startFromRandomUnitary, const double gradThreshold=EDMISTONRUED_gradThreshold, const int maxIter=EDMISTONRUED_maxIter) |
| Maximize the Edmiston-Ruedenberg cost function. More... | |
| void | FiedlerExchange (const int maxlinsize, double *temp1, double *temp2) |
| Permute the orbitals so that the bandwidth of the exchange matrix is (approximately) minimized (per irrep) More... | |
| void | FiedlerGlobal (int *dmrg2ham) const |
| Permute the orbitals so that the bandwidth of the exchange matrix is (approximately) minimized. More... | |
| DMRGSCFunitary * | getUnitary () |
| Get the pointer to the unitary to use in DMRGSCF. More... | |
EdmistonRuedenberg class.
DMRG is not invariant with respect to orbital choice and ordering [LOC1]. An MPS introduces an artificial correlation length. Highly correlated orbitals should be placed close to each other for optimal DMRG performance. The correlation between localized orbitals in extended molecules decreases with increasing spatial separation. The exchange matrix directly reflects orbital overlap and separation. Minimizing its bandwidth yields a good ordering for extended molecules [LOC2, LOC3].
Physics notation is assumed for the two-body matrix elements (the electron repulsion integrals with eightfold permutation symmetry):
![\[ v_{ij;kl} = \left( i(\vec{r}_1) j(\vec{r}_2) \left| \frac{1}{\mid \vec{r}_1 - \vec{r}_2 \mid} \right| k(\vec{r}_1) l(\vec{r}_2) \right). \]](form_143.png)
Edmiston and Ruedenberg proposed to maximize the cost function
![\[ I = \sum\limits_i v_{ii;ii} \]](form_144.png)
in order to obtain localized orthonormal orbitals [LOC4]. When the spatial extent of an orbital is small, its self-repulsion will indeed be high. CheMPS2 obtains localized orbitals (per irrep) with an augmented Hessian Newton-Raphson maximization of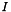 
, which can be called with the function CheMPS2::EdmistonRuedenberg::Optimize.
The orbitals which maximize the cost function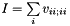 
can be parametrized with an orthogonal matrix 
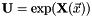(see CheMPS2::CASSCF):
![\[ I(\mathbf{U}) = \sum\limits_{ijklm} \left[ \mathbf{U} \right]_{ij} \left[ \mathbf{U} \right]_{ik} \left[ \mathbf{U} \right]_{il} \left[ \mathbf{U} \right]_{im} v_{jk;lm}. \]](form_148.png)
The following derivatives from Ref. [LOC5] are useful:
![\[ \left[ \frac{\partial \left[ \mathbf{U} \right]_{\alpha \beta}}{\partial x_{pq}} \right]_0 = \delta_{p \alpha} \delta_{q \beta} - \delta_{q \alpha} \delta_{p \beta}, \]](form_149.png)
![\begin{eqnarray*} 2 \left[ \frac{\partial^2 \left[ \mathbf{U} \right]_{\alpha \beta}}{\partial x_{pq} \partial x_{rs}} \right]_0 & = & \delta_{qr} (\delta_{p \alpha} \delta_{s \beta} + \delta_{s \alpha} \delta_{p \beta} ) \\ & - & \delta_{pr} (\delta_{q \alpha} \delta_{s \beta} + \delta_{s \alpha} \delta_{q \beta} ) \\ & - & \delta_{qs} (\delta_{p \alpha} \delta_{r \beta} + \delta_{r \alpha} \delta_{p \beta} ) \\ & + & \delta_{ps} (\delta_{q \alpha} \delta_{r \beta} + \delta_{r \alpha} \delta_{q \beta} ), \end{eqnarray*}](form_150.png)
in which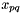 
is the element in 
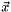which corresponds to ![$\left[ \mathbf{X} \right]_{pq}$](form_151.png)
. Keeping the eightfold permutation symmetry of 
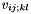in mind, the gradient of 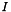with respect to orbital rotations is
![\[ \left[ \frac{\partial I}{\partial x_{pq}} \right]_0 = 4 (v_{pp;pq} - v_{qq;qp}), \]](form_153.png)
and the Hessian
![\begin{eqnarray*} \left[ \frac{\partial^2 I}{\partial x_{pq} \partial x_{rs}} \right]_0 & = & \delta_{pr} (8v_{pp;qs} + 4v_{pq;ps} - 2v_{qq;qs} - 2v_{ss;sq}) \\ & + & \delta_{qs} (8v_{qq;pr} + 4v_{qp;qr} - 2v_{pp;pr} - 2v_{rr;rp}) \\ & - & \delta_{ps} (8v_{pp;qr} + 4v_{pq;pr} - 2v_{qq;qr} - 2v_{rr;rq})\\ & - & \delta_{qr} (8v_{qq;ps} + 4v_{qp;qs} - 2v_{pp;ps} - 2v_{ss;sp}). \end{eqnarray*}](form_154.png)
Once localized orbitals are obtained, they can be ordered so that the bandwidth of the exchange matrix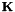 
is minimal. This matrix has only nonnegative entries [LOC6]:
![\[ \left[ \mathbf{K} \right]_{ij} = v_{ij;ji} \geq 0. \]](form_156.png)
A fast approximate bandwidth minimization is obtained by the so-called Fiedler vector [LOC7, LOC8, LOC9, LOC10]. Consider the minimization of the cost function
![\[ F(\vec{z}) ~ = ~ \frac{1}{2} \sum\limits_{k \neq l} \left[ \mathbf{K} \right]_{kl} (z_k - z_l)^2 ~ \geq 0, \]](form_157.png)
where the (continuous) variable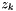 
denotes the optimal position of orbital 
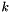. In order to fix translational invariance and normalization of the solution, the constraints 
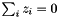and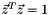 
are imposed. The cost function can be rewritten as
![\[ F(\vec{z}) ~ = ~ \vec{z}^T \mathbf{L} \vec{z} ~ \geq 0, \]](form_162.png)
with the symmetric and positive semidefinite Laplacian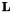 
:
![\[ \left[ \mathbf{L} \right]_{k \neq l} = - \left[ \mathbf{K} \right]_{kl}, \]](form_164.png)
![\[ \left[ \mathbf{L} \right]_{k k} = \sum\limits_{m \neq k} \left[ \mathbf{K} \right]_{km}. \]](form_165.png)
The constant vector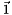 
is an eigenvector of 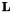with eigenvalue 0, which is discarded due to the translational invariance constraint. When the exchange matrix 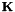is not block-diagonal, all other eigenvalues are positive. The eigenvector with smallest nonzero eigenvalue is the Fiedler vector, the solution to the constrained minimization of 
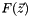[LOC7, LOC8, LOC9, LOC10]. When the indices of the orbitals are permuted so that they are ordered according to the continuous variables in the Fiedler vector, a fast approximate bandwidth minimization of the exchange matrix 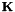is performed. CheMPS2 orders the localized orbitals according to the Fiedler vector of the exchange matrix, which is performed in the function CheMPS2::EdmistonRuedenberg::FiedlerExchange.
[LOC1] S. Wouters and D. Van Neck, European Physical Journal D 68, 272 (2014). http://dx.doi.org/10.1140/epjd/e2014-50500-1
[LOC2] W. Mizukami, Y. Kurashige and T. Yanai, Journal of Chemical Theory and Computation 9, 401-407 (2013). http://dx.doi.org/10.1021/ct3008974
[LOC3] N. Nakatani and G.K.-L. Chan, Journal of Chemical Physics 138, 134113 (2013). http://dx.doi.org/10.1063/1.4798639
[LOC4] C. Edmiston and K. Ruedenberg, Reviews of Modern Physics 35, 457-464 (1963). http://dx.doi.org/10.1103/RevModPhys.35.457
[LOC5] P.E.M. Siegbahn, J. Almlof, A. Heiberg and B.O. Roos, Journal of Chemical Physics 74, 2384-2396 (1981). http://dx.doi.org/10.1063/1.441359
[LOC6] A. Auerbach, Interacting Electrons and Quantum Magnetism, Springer, Heidelberg, 1994.
[LOC7] M. Fiedler, Czechoslovak Mathematical Journal 23, 298-305 (1973). http://dml.cz/dmlcz/101168
[LOC8] M. Fiedler, Czechoslovak Mathematical Journal 25, 619-633 (1975). http://dml.cz/dmlcz/101357
[LOC9] G. Barcza, O. Legeza, K. H. Marti, M. Reiher, Physical Review A 83, 012508 (2011). http://dx.doi.org/10.1103/PhysRevA.83.012508
[LOC10] M.W. Berry, Fiedler ordering, http://web.eecs.utk.edu/~mberry/order/node9.html (1996).
In the Boys localization method, the cost function
![\[ J = \frac{1}{2} \sum\limits_{ij} \left( \braket{ \phi_i \mid \vec{r} \mid \phi_i } - \braket{ \phi_j \mid \vec{r} \mid \phi_j } \right)^2 = \frac{1}{2} \sum\limits_{ij} \left( \vec{r}_{ii} - \vec{r}_{jj} \right)^2 \]](form_168.png)
is maximized. With an orthogonal orbital rotation 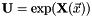, the cost function becomes
![\[ J(\mathbf{U}) = \frac{1}{2} \sum\limits_{i,j} \left( \left[ \mathbf{U} \right]_{i\alpha} \left[ \mathbf{U} \right]_{i\beta} \vec{r}_{\alpha\beta} - \left[ \mathbf{U} \right]_{j\alpha} \left[ \mathbf{U} \right]_{j\beta} \vec{r}_{\alpha\beta} \right)^2. \]](form_169.png)
The gradient and hessian of J with respect to orbital rotations are given by:
![\begin{eqnarray*} \left[ \frac{\partial J}{\partial x_{pq}} \right]_0 & = & 2 N_{orb} \left[ \left( \vec{r}_{pq} + \vec{r}_{qp} \right).\left( \vec{r}_{pp} - \vec{r}_{qq} \right) \right] \\ \left[ \frac{\partial^2 J}{\partial x_{pq} \partial x_{rs}} \right]_0 & = & 2 N_{orb} \left( \delta_{pr} + \delta_{qs} - \delta_{qr} - \delta_{ps} \right) \left[ \left( \vec{r}_{pq} + \vec{r}_{qp} \right).\left( \vec{r}_{rs} + \vec{r}_{sr} \right) \right] \\ & + & N_{orb} \delta_{pr} \left[ \left( \vec{r}_{qs} + \vec{r}_{sq} \right).\left( 2 \vec{r}_{pp} - \vec{r}_{qq} - \vec{r}_{ss} \right) \right] \\ & + & N_{orb} \delta_{qs} \left[ \left( \vec{r}_{pr} + \vec{r}_{rp} \right).\left( 2 \vec{r}_{qq} - \vec{r}_{pp} - \vec{r}_{rr} \right) \right] \\ & - & N_{orb} \delta_{qr} \left[ \left( \vec{r}_{ps} + \vec{r}_{sp} \right).\left( 2 \vec{r}_{qq} - \vec{r}_{pp} - \vec{r}_{ss} \right) \right] \\ & - & N_{orb} \delta_{ps} \left[ \left( \vec{r}_{qr} + \vec{r}_{rq} \right).\left( 2 \vec{r}_{pp} - \vec{r}_{qq} - \vec{r}_{rr} \right) \right]. \end{eqnarray*}](form_170.png)
(Written down here for future reference.)
Definition at line 126 of file EdmistonRuedenberg.h.
| CheMPS2::EdmistonRuedenberg::EdmistonRuedenberg | ( | const FourIndex * | Vmat, |
| const int | group, | ||
| const int | printLevelIn = 1 |
||
| ) |
Constructor.
| Vmat | The active space two-electron integrals |
| group | The group number |
| printLevelIn | If 0: nothing is printed. If 1: info at beginning and end. If >1: intermediary info as well. |
Definition at line 34 of file EdmistonRuedenberg.cpp.
Here is the call graph for this function:| void CheMPS2::EdmistonRuedenberg::FiedlerExchange | ( | const int | maxlinsize, |
| double * | temp1, | ||
| double * | temp2 | ||
| ) |
Permute the orbitals so that the bandwidth of the exchange matrix is (approximately) minimized (per irrep)
| maxlinsize | max(dim(irrep(Ham))) |
| temp1 | Work memory of at least 4*max(dim(irrep(Ham)))^2 |
| temp2 | Work memory of at least 4*max(dim(irrep(Ham)))^2 |
Definition at line 367 of file EdmistonRuedenberg.cpp.
Here is the call graph for this function: Here is the caller graph for this function:| void CheMPS2::EdmistonRuedenberg::FiedlerGlobal | ( | int * | dmrg2ham | ) | const |
Permute the orbitals so that the bandwidth of the exchange matrix is (approximately) minimized.
| dmrg2ham | At exit, dmrg2ham contains the new orbital ordering |
Definition at line 432 of file EdmistonRuedenberg.cpp.
Here is the call graph for this function: Here is the caller graph for this function:| CheMPS2::DMRGSCFunitary * CheMPS2::EdmistonRuedenberg::getUnitary | ( | ) |
Get the pointer to the unitary to use in DMRGSCF.
Definition at line 143 of file EdmistonRuedenberg.cpp.
Here is the call graph for this function: Here is the caller graph for this function:| double CheMPS2::EdmistonRuedenberg::Optimize | ( | double * | temp1, |
| double * | temp2, | ||
| const bool | startFromRandomUnitary, | ||
| const double | gradThreshold = EDMISTONRUED_gradThreshold, |
||
| const int | maxIter = EDMISTONRUED_maxIter |
||
| ) |
Maximize the Edmiston-Ruedenberg cost function.
| temp1 | Work memory of at least max(dim(irrep(Ham)))^4 |
| temp2 | Work memory of at least max(dim(irrep(Ham)))^4 |
| startFromRandomUnitary | The name of the variable says it all. Useful if the point group symmetry is reduced to make use of locality in the DMRG calculations, but when the molecular orbitals still belong to the full point group. |
| gradThreshold | Stop if the norm of the gradient is smaller than this value |
| maxIter | Stop if maxIter iterations have been performed (when gradThreshold is not reached) |
Definition at line 66 of file EdmistonRuedenberg.cpp.
Here is the call graph for this function: Here is the caller graph for this function:
1.8.11 
