#include <DMRGSCFunitary.h>

Inheritance diagram for CheMPS2::DMRGSCFunitary:

Collaboration diagram for CheMPS2::DMRGSCFunitary:

Public Member Functions
	DMRGSCFunitary (const DMRGSCFindices *iHandler)
	Constructor. More...

virtual	~DMRGSCFunitary ()
	Destructor.

int	getNumVariablesX () const
	Get the number of variables in the x-parametrization of the unitary update. More...

void	updateUnitary (double workmem1, double workmem2, double *vector, const bool multiply, const bool compact)
	Update the unitary transformation. More...

void	rotateActiveSpaceVectors (double eigenvecs, double work)
	Rotate the unitary matrix. More...

void	CheckDeviationFromUnitary (double *work) const
	Calculate the two-norm of U^T*U - I. More...

void	getLog (double vector, double temp1, double *temp2) const
	Obtain the logarithm of the unitary matrix. More...

void	makeSureAllBlocksDetOne (double temp1, double temp2)
	Orbitals are defined up to a phase factor. Make sure that the logarithm of each block of the unitary has determinant 1. More...

void	saveU (const string filename=DMRGSCF_unitary_storage_name) const
	Save the unitary to disk. More...

void	loadU (const string filename=DMRGSCF_unitary_storage_name)
	Load the unitary from disk. More...

Public Member Functions inherited from CheMPS2::DMRGSCFmatrix
	DMRGSCFmatrix (const DMRGSCFindices *iHandler)
	Constructor. More...

virtual	~DMRGSCFmatrix ()
	Destructor.

void	clear ()
	Clear the matrix.

void	identity ()
	Make this matrix the identity matrix.

void	set (const int irrep, const int p, const int q, const double val)
	Set an element. More...

double	get (const int irrep, const int p, const int q) const
	Get an element. More...

double *	getBlock (const int irrep)
	Get a matrix block. More...

double	rms_deviation (const DMRGSCFmatrix *other) const
	Get the RMS deviation with another DMRGSCFmatrix. More...

Additional Inherited Members
Static Public Member Functions inherited from CheMPS2::DMRGSCFmatrix
static void	write (const string filename, const DMRGSCFindices idx, double *storage)
	Write a DMRGSCFmatrix to disk. More...

static void	read (const string filename, const int n_irreps, double **storage)
	Read the DMRGSCFmatrix from disk. More...

Protected Attributes inherited from CheMPS2::DMRGSCFmatrix
const DMRGSCFindices *	iHandler
	The information on the occupied, active, and virtual spaces.

double **	entries
	The matrix entries.

int	num_irreps
	The number of irreps.

Detailed Description

DMRGSCFunitary class.

Author: Sebastian Wouters sebas.nosp@m.tian.nosp@m.woute.nosp@m.rs@g.nosp@m.mail..nosp@m.com

Date: July 11, 2014

The DMRGSCFunitary class is a storage and manipulation class for the DMRGSCF orthogonal orbital rotation matrix. This matrix is blockdiagonal in the irreducible representations, and is formed by stepwise multiplying in new unitary rotations due to the augmented Hessian Newton-Raphson algorithm, see CheMPS2::CASSCF.

Exponential of a skew-symmetric matrix

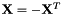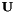The exponential of a real-valued skew-symmetric matrix $\mathbf{X} = -\mathbf{X}^T$ is an orthogonal matrix $\mathbf{U}$ :

$\mathbf{U}^T \mathbf{U} = \exp(\mathbf{X}^T) \exp(\mathbf{X}) = \exp(- \mathbf{X}) \exp(\mathbf{X}) = \mathbf{I}.$

A real-valued skew-symmetric matrix 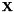$\mathbf{X}$ has purely imaginary eigenvalues, which come in complex conjugate pairs 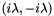$(i \lambda, -i\lambda)$ . For matrices of odd dimension, there should hence always be one eigenvalue 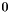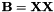$0$ . $\mathbf{B} = \mathbf{X} \mathbf{X}$ is then a symmetric matrix with nonpositive real-valued eigenvalues 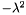$-\lambda^2$ . Nonzero eigenvalues of 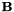$\mathbf{B}$ occur twice. 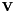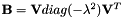The eigenvectors $\mathbf{V}$ of $\mathbf{B} = \mathbf{V} diag(-\lambda^2) \mathbf{V}^T$ allow to make 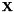$\mathbf{X}$ block-diagonal. 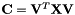$\mathbf{C} = \mathbf{V}^T \mathbf{X} \mathbf{V}$ is skew-symmetric. Moreover, 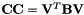$\mathbf{C}\mathbf{C} = \mathbf{V}^T \mathbf{B} \mathbf{V}$ is diagonal: 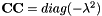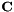$\mathbf{C}\mathbf{C} = diag(-\lambda^2)$ . 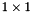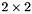$\mathbf{C}$ is hence block-diagonal with $1 \times 1$ blocks $\left[0\right]$ and $2 \times 2$ blocks

$\left[ \begin{array}{cc} 0 & \lambda \\ -\lambda & 0 \end{array} \right].$

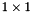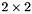The exponential of the $1 \times 1$ block $\left[0\right]$ is $\left[1\right]$ , and the exponential of the $2 \times 2$ block is

$\exp \left[ \begin{array}{cc} 0 & \lambda \\ -\lambda & 0 \end{array} \right] = \left[ \begin{array}{cc} \cos(\lambda) & \sin(\lambda) \\ -\sin(\lambda) & \cos(\lambda) \end{array} \right].$

The matrix 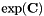$\exp(\mathbf{C})$ can hence be easily calculated blockwise. The exponential of 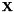$\mathbf{X}$ is then obtained as 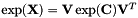$\exp(\mathbf{X}) = \mathbf{V} \exp(\mathbf{C}) \mathbf{V}^T$ . It is calculated by the function CheMPS2::DMRGSCFunitary::updateUnitary.

Logarithm of a special orthogonal matrix

The reverse problem of finding a (nonunique) real-valued logarithm of a special orthogonal matrix 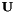$\mathbf{U}$ can be performed similarly. Since 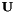$\mathbf{U}$ is orthogonal (and hence norm-preserving), its eigenvalues all have norm 1:

$\mathbf{U} = \mathbf{V}_{U} diag(e^{i \theta}) \mathbf{V}_{U}^{\dagger} = \mathbf{V}_{U}^* diag(e^{-i \theta}) \mathbf{V}_{U}^{T},$

$\mathbf{U}^T = \mathbf{V}_{U}^* diag(e^{i \theta}) \mathbf{V}_{U}^{T} = \mathbf{V}_{U} diag(e^{-i \theta}) \mathbf{V}_{U}^{\dagger}.$

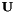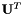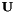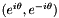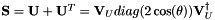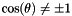For the second equalities, complex conjugation of the real-valued matrices $\mathbf{U}$ and $\mathbf{U}^T$ is used. The eigenvalues of $\mathbf{U}$ hence come in complex conjugate pairs $(e^{i \theta}, e^{-i \theta})$ . Consider the symmetric matrix $\mathbf{S} = \mathbf{U} + \mathbf{U}^T = \mathbf{V}_{U} diag(2\cos(\theta) ) \mathbf{V}_{U}^{\dagger}$ . If $\cos(\theta) \neq \pm 1$ , the eigenvalue 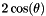$2\cos(\theta)$ occurs twice. For matrices of odd dimension 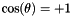$\cos(\theta)=+1$ always occurs an odd number of times. Construct the symmetric matrix 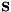$\mathbf{S}$ and diagonalize it (real-valued) as 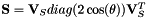$\mathbf{S} = \mathbf{V}_{S} diag(2\cos(\theta)) \mathbf{V}_{S}^T$ . 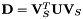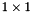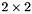The matrix $\mathbf{D} = \mathbf{V}_{S}^T \mathbf{U} \mathbf{V}_{S}$ is also a special orthogonal matrix with $1 \times 1$ blocks $\left[ \pm 1 \right]$ and $2 \times 2$ blocks

$\left[ \begin{array}{cc} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{array} \right].$

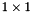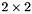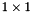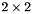Because we consider special orthogonal matrices, the $1 \times 1$ blocks $\left[ -1 \right]$ always occur an even number of times, and they can hence be considered as a special case of the $2 \times 2$ blocks. If we choose the branchcut for the logarithm on the negative real axis, the logarithm of the $1 \times 1$ block $\left[ 1 \right]$ is $\left[ 0 \right]$ and the logarithm of the $2\times 2$ block is

$\log \left[ \begin{array}{cc} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{array} \right] = \left[ \begin{array}{cc} 0 & \theta \\ -\theta & 0 \end{array} \right],$

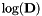with $\theta \in \left[ -\pi, \pi \right]$ . The matrix $\log(\mathbf{D})$ can hence be easily calculated blockwise. The logarithm of 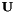$\mathbf{U}$ is then obtained as 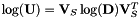$\log(\mathbf{U}) = \mathbf{V}_{S} \log(\mathbf{D}) \mathbf{V}_{S}^T$ . It is calculated by the function CheMPS2::DMRGSCFunitary::getLog.

Definition at line 70 of file DMRGSCFunitary.h.

Constructor & Destructor Documentation

CheMPS2::DMRGSCFunitary::DMRGSCFunitary ( const DMRGSCFindices * iHandler )

Constructor.

Parameters

iHandler The DMRGSCF indices

Definition at line 31 of file DMRGSCFunitary.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

Member Function Documentation

void CheMPS2::DMRGSCFunitary::CheckDeviationFromUnitary ( double * work ) const

Calculate the two-norm of U^T*U - I.

Parameters

work	Work memory

Definition at line 244 of file DMRGSCFunitary.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

void CheMPS2::DMRGSCFunitary::getLog	(	double *	vector,
		double *	temp1,
		double *	temp2
	)		const

Obtain the logarithm of the unitary matrix.

Parameters

vector	Where the logarithm should be stored
temp1	Work memory of at least 4*max(dim(irrep(Ham)))^2
temp2	Work memory of at least 4*max(dim(irrep(Ham)))^2

Definition at line 319 of file DMRGSCFunitary.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

int CheMPS2::DMRGSCFunitary::getNumVariablesX ( ) const

Get the number of variables in the x-parametrization of the unitary update.

Returns: The number of unique variables in the x-matrix

Definition at line 60 of file DMRGSCFunitary.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

void CheMPS2::DMRGSCFunitary::loadU ( const string filename = DMRGSCF_unitary_storage_name )

Load the unitary from disk.

Parameters

filename Filename to load the unitary from

Definition at line 437 of file DMRGSCFunitary.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

void CheMPS2::DMRGSCFunitary::makeSureAllBlocksDetOne	(	double *	temp1,
		double *	temp2
	)

Orbitals are defined up to a phase factor. Make sure that the logarithm of each block of the unitary has determinant 1.

Parameters

temp1	Work memory of at least 4*max(dim(irrep(Ham)))^2
temp2	Work memory of at least 4*max(dim(irrep(Ham)))^2

Definition at line 403 of file DMRGSCFunitary.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

void CheMPS2::DMRGSCFunitary::rotateActiveSpaceVectors	(	double *	eigenvecs,
		double *	work
	)

Rotate the unitary matrix.

Parameters

eigenvecs	The rotation vectors, in a memory block of size nOrbDMRG^2
work	Work memory, with size 2*max(dim(irrep(Ham)))^2

Definition at line 210 of file DMRGSCFunitary.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

void CheMPS2::DMRGSCFunitary::saveU ( const string filename = DMRGSCF_unitary_storage_name ) const

Save the unitary to disk.

Parameters

filename Filename to store the unitary to

Definition at line 431 of file DMRGSCFunitary.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

void CheMPS2::DMRGSCFunitary::updateUnitary	(	double *	workmem1,
		double *	workmem2,
		double *	vector,
		const bool	multiply,
		const bool	compact
	)

Update the unitary transformation.

Parameters

workmem1	Work memory of at least 4*max(dim(irrep(Ham)))^2
workmem2	Work memory of at least 4*max(dim(irrep(Ham)))^2
vector	The elements in X
multiply	Boolean whether exp(X)U or exp(X) should become the new U. If multiply==true, U <– exp(X)U. If multiply==false, U <– exp(X).
compact	Boolean which indicates how the elements X are stored

Definition at line 117 of file DMRGSCFunitary.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

The documentation for this class was generated from the following files:

Public Member Functions

Additional Inherited Members

Detailed Description

Exponential of a skew-symmetric matrix

Logarithm of a special orthogonal matrix

Constructor & Destructor Documentation

Member Function Documentation