 |
CheMPS2
|
 |
CheMPS2
|
#include <CASSCF.h>
Public Member Functions | |
| CASSCF (Hamiltonian *ham_in, int *docc, int *socc, int *nocc, int *ndmrg, int *nvirt, const string tmp_folder=CheMPS2::defaultTMPpath) | |
| Constructor. More... | |
| virtual | ~CASSCF () |
| Destructor. | |
| int | get_num_irreps () |
| Get the number of irreps. More... | |
| double | solve (const int Nelectrons, const int TwoS, const int Irrep, ConvergenceScheme *OptScheme, const int rootNum, DMRGSCFoptions *scf_options) |
| Do the CASSCF cycles with the augmented Hessian Newton-Raphson method. More... | |
| double | caspt2 (const int Nelectrons, const int TwoS, const int Irrep, ConvergenceScheme *OptScheme, const int rootNum, DMRGSCFoptions *scf_options, const double IPEA, const double IMAG, const bool PSEUDOCANONICAL, const bool CHECKPOINT=false, const bool CUMULANT=false) |
| Calculate the caspt2 correction energy for a converged casscf wavefunction. More... | |
Static Public Member Functions | |
| static void | deleteStoredUnitary (const string filename=CheMPS2::DMRGSCF_unitary_storage_name) |
| CASSCF unitary rotation remove call. | |
| static void | deleteStoredDIIS (const string filename=CheMPS2::DMRGSCF_diis_storage_name) |
| CASSCF DIIS vectors remove call. | |
| static void | buildFmat (DMRGSCFmatrix *localFmat, const DMRGSCFmatrix *localTmat, const DMRGSCFmatrix *localJKocc, const DMRGSCFmatrix *localJKact, const DMRGSCFindices *localIdx, const DMRGSCFintegrals *theInts, double *local2DM, double *local1DM) |
| Build the F-matrix (Eq. (11) in the Siegbahn paper [CAS3]) More... | |
| static void | buildWtilde (DMRGSCFwtilde *localwtilde, const DMRGSCFmatrix *localTmat, const DMRGSCFmatrix *localJKocc, const DMRGSCFmatrix *localJKact, const DMRGSCFindices *localIdx, const DMRGSCFintegrals *theInts, double *local2DM, double *local1DM) |
| Build the Wtilde-matrix (Eq. (20b) in the Siegbahn paper [CAS3]) More... | |
| static void | augmentedHessianNR (DMRGSCFmatrix *localFmat, DMRGSCFwtilde *localwtilde, const DMRGSCFindices *localIdx, const DMRGSCFunitary *localUmat, double *theupdate, double *updateNorm, double *gradNorm) |
| Calculate the augmented Hessian Newton-Raphson update for the orthogonal orbital rotation matrix. More... | |
| static void | copy2DMover (TwoDM *theDMRG2DM, const int LAS, double *two_dm) |
| Copy over the DMRG 2-RDM. More... | |
| static void | setDMRG1DM (const int num_elec, const int LAS, double *one_dm, double *two_dm) |
| Construct the 1-RDM from the 2-RDM. More... | |
| static void | copy_active (double *origin, DMRGSCFmatrix *result, const DMRGSCFindices *idx, const bool one_rdm) |
| Copy a one-orbital quantity from array format to DMRGSCFmatrix format. More... | |
| static void | copy_active (const DMRGSCFmatrix *origin, double *result, const DMRGSCFindices *idx) |
| Copy a one-orbital quantity from DMRGSCFmatrix format to array format. More... | |
| static void | fillLocalizedOrbitalRotations (DMRGSCFunitary *umat, DMRGSCFindices *idx, double *eigenvecs) |
| From an Edmiston-Ruedenberg active space rotation, fetch the eigenvectors and store them in eigenvecs. More... | |
| static void | block_diagonalize (const char space, const DMRGSCFmatrix *Mat, DMRGSCFunitary *Umat, double *work1, double *work2, const DMRGSCFindices *idx, const bool invert, double *two_dm, double *three_dm, double *contract) |
| Block-diagonalize Mat. More... | |
| static void | construct_fock (DMRGSCFmatrix *Fock, const DMRGSCFmatrix *Tmat, const DMRGSCFmatrix *Qocc, const DMRGSCFmatrix *Qact, const DMRGSCFindices *idx) |
| Construct the Fock matrix. More... | |
| static double | deviation_from_blockdiag (DMRGSCFmatrix *matrix, const DMRGSCFindices *idx) |
| Return the RMS deviation from block-diagonal. More... | |
| static void | write_f4rdm_checkpoint (const string f4rdm_file, int *hamorb1, int *hamorb2, const int tot_dmrg_power6, double *contract) |
| Write the checkpoint file for the contraction of the generalized Fock operator with the 4-RDM to disk. More... | |
| static bool | read_f4rdm_checkpoint (const string f4rdm_file, int *hamorb1, int *hamorb2, const int tot_dmrg_power6, double *contract) |
| Read the checkpoint file for the contraction of the generalized Fock operator with the 4-RDM from disk. More... | |
| static void | fock_dot_4rdm (double *fockmx, CheMPS2::DMRG *dmrgsolver, CheMPS2::Hamiltonian *ham, int next_orb1, int next_orb2, double *work, double *result, const bool CHECKPOINT, const bool PSEUDOCANONICAL) |
| Build the contraction of the fock matrix with the 4-RDM. More... | |
CASSCF class.
In methods which use a FCI solver, this solver can be replaced by DMRG. DMRG allows for an efficient extraction of the 2-RDM [CAS1, CAS2]. The 2-RDM of the active space is required in the complete active space self-consistent field (CASSCF) method to compute the gradient and the Hessian with respect to orbital rotations [CAS3]. It is therefore natural to introduce a CASSCF variant with DMRG as active space solver, called DMRG-SCF [CAS2, CAS4, CAS5], which allows to treat static correlation in large active spaces. In CheMPS2, I have implemented the augmented Hessian Newton-Raphson DMRG-SCF method, with exact Hessian [CAS5, CAS6]. It can be called with the function CheMPS2::CASSCF::doCASSCFnewtonraphson.
The calculation of the orbital gradient and Hessian for DMRG-SCF is based on [CAS3]. The basic idea is to express the energy with the unitary group generators:
![\begin{eqnarray*} \hat{E}_{pq} & = & \sum\limits_{\sigma} \hat{a}^{\dagger}_{p \sigma} \hat{a}_{q \sigma} \\ \left[ \hat{E}_{pq} , \hat{E}_{rs} \right] & = & \delta_{qr} \hat{E}_{ps} - \delta_{ps} \hat{E}_{rq} \\ \hat{E}^{-}_{pq} & = & \hat{E}_{pq} - \hat{E}_{qp} \\ \hat{T} & = & \sum\limits_{p<q} x_{pq} \hat{E}^{-}_{pq} \\ E(\vec{x}) & = & \braket{0 | e^{\hat{T}} \hat{H} e^{-\hat{T}} | 0 } \\ \left. \frac{\partial E(\vec{x})}{\partial x_{ij}} \right|_{0} & = & \braket{ 0 | \left[ \hat{E}_{ij}^{-}, \hat{H} \right] | 0 } \\ \left. \frac{\partial^2 E(\vec{x})}{\partial x_{ij} \partial x_{kl}} \right|_{0} & = & \frac{1}{2} \braket{ 0 | \left[ \hat{E}_{ij}^{-}, \left[ \hat{E}_{kl}^{-}, \hat{H} \right] \right] | 0 } + \frac{1}{2} \braket{ 0 | \left[ \hat{E}_{kl}^{-}, \left[ \hat{E}_{ij}^{-}, \hat{H} \right] \right] | 0 } \end{eqnarray*}](form_0.png)
The variables 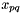 only connect orbitals with the same irrep (
only connect orbitals with the same irrep ( 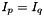 ). Assuming that DMRG is exact,
). Assuming that DMRG is exact, 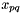 in addition only connects orbitals when they belong to different occupation blocks: occupied, active, virtual. With some algebra, the derivatives can be rewritten. Real-valued symmetric one-electron integrals
in addition only connects orbitals when they belong to different occupation blocks: occupied, active, virtual. With some algebra, the derivatives can be rewritten. Real-valued symmetric one-electron integrals 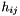 and real-valued eightfold permutation symmetric two-electron integrals
and real-valued eightfold permutation symmetric two-electron integrals 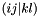 are assumed (chemical notation for the latter).
are assumed (chemical notation for the latter).
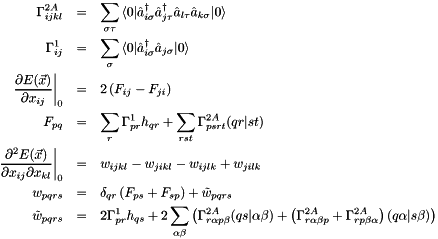
In the calculation of 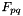 , the indices
, the indices 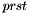 can only be occupied or active due to their appearance in the density matrices, and the only index which can be virtual is hence
can only be occupied or active due to their appearance in the density matrices, and the only index which can be virtual is hence 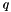 . Moreover, due to the irrep symmetry of the integrals and density matrices,
. Moreover, due to the irrep symmetry of the integrals and density matrices, 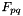 is diagonal in the irreps:
is diagonal in the irreps: 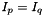 . Alternatively, this can be understood by the fact that
. Alternatively, this can be understood by the fact that 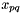 only connects orbitals with the same irrep.
only connects orbitals with the same irrep.
In the calculation of 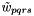 , the indices
, the indices  can only be occupied or active due to their appearance in the density matrices, and the only indices which can be virtual are hence
can only be occupied or active due to their appearance in the density matrices, and the only indices which can be virtual are hence 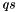 . Together with the remark for
. Together with the remark for 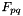 , this can save time for the two-electron integral rotation. Moreover, as
, this can save time for the two-electron integral rotation. Moreover, as 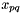 only connects orbitals with the same irrep,
only connects orbitals with the same irrep, 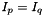 and
and 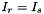 in
in 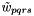 .
.
By rewriting the density matrices, the calculation of 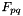 and
and 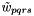 can be simplified. In the following, occ and act denote the doubly occupied and active orbital spaces, respectively.
can be simplified. In the following, occ and act denote the doubly occupied and active orbital spaces, respectively.
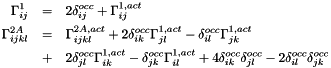
Define the following symmetric charge (Coulomb + exchange) matrices:
![\begin{eqnarray*} Q^{occ}_{ij} & = & \sum\limits_{s \in occ} \left[ 2 (ij | ss) - (is | js ) \right] \\ Q^{act}_{ij} & = & \sum\limits_{st \in act} \frac{1}{2} \Gamma^{1,act}_{st} \left[ 2 (ij | st) - (is | jt ) \right] \end{eqnarray*}](form_15.png)
They can be calculated efficiently by (1) rotating the occupied and active density matrices from the current basis to the original basis, (2) contracting the rotated density matrices with the two-electron integrals in the original basis, and (3) rotating these contractions to the current basis. The constant part and the one-electron integrals of the active space Hamiltonian are:
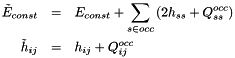
The calculation of 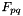 boils down to:
boils down to:
![\begin{eqnarray*} p \in occ & : & F_{pq} = 2 \left( h_{qp} + Q^{occ}_{qp} + Q^{act}_{qp} \right) \\ p \in act & : & F_{pq} = \sum\limits_{r \in act} \Gamma^{1,act}_{pr} \left[ h_{qr} + Q^{occ}_{qr} \right] + \sum\limits_{rst \in act} \Gamma^{2A,act}_{psrt} (qr | st) \end{eqnarray*}](form_17.png)
And the calculation of 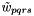 (remember that
(remember that 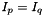 and
and 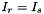 ):
):
![\begin{eqnarray*} (p,r) & \in & (occ,occ) : \tilde{w}_{pqrs} \\ & = & 4 \delta_{pr}^{occ} \left[ h_{qs} + Q^{occ}_{qs} + Q^{act}_{qs} \right] \\ & + & 4 \left[ 4 (qp | sr) - ( qs | pr ) - ( qr | sp ) \right] \\ (p,r) & \in & (act,act) : \tilde{w}_{pqrs} = 2 \Gamma^{1,act}_{rp} \left[ h_{qs} + Q^{occ}_{qs} \right] \\ & + & 2 \sum\limits_{\alpha\beta \in act} \left[ \Gamma^{2A,act}_{r \alpha p \beta} (qs | \alpha \beta ) + \left( \Gamma^{2A,act}_{r \alpha \beta p} + \Gamma^{2A,act}_{r p \beta \alpha} \right) (q \alpha | s \beta ) \right] \\ (p,r) & \in & (act,occ) : \tilde{w}_{pqrs} \\ & = & 2 \sum\limits_{\alpha \in act} \Gamma^{1,act}_{\alpha p} \left[ 4 (q \alpha | s r) - (qs | \alpha r) - (qr | s \alpha) \right] \\ (p,r) & \in & (occ,act) : \tilde{w}_{pqrs} \\ & = & 2 \sum\limits_{\beta \in act} \Gamma^{1,act}_{r \beta} \left[ 4 (q p | s \beta) - (qs | p \beta) - (q \beta | sp) \right] \end{eqnarray*}](form_18.png)
The CASSCF energy is a function of 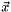 . Up to second order, the energy is given by
. Up to second order, the energy is given by
![\[ E(\vec{x}) = \braket{0 | e^{\hat{T}(\vec{x})} \hat{H} e^{-\hat{T}(\vec{x})} | 0 } \approx E(0) + \vec{x}^T \vec{g} + \frac{1}{2} \vec{x}^T \mathbf{H} \vec{x}. \]](form_20.png)
The vector 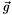 is the gradient and the matrix
is the gradient and the matrix 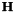 the Hessian for orbital rotations [CAS3]. They have been described in the previous section. The minimum of
the Hessian for orbital rotations [CAS3]. They have been described in the previous section. The minimum of 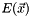 is found at
is found at 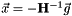 . The variables
. The variables 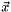 parametrize an additional orbital rotation
parametrize an additional orbital rotation 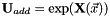 , with
, with 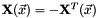 a real-valued skew-symmetric matrix. The additional orbital rotation
a real-valued skew-symmetric matrix. The additional orbital rotation 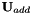 transforms the current orbitals
transforms the current orbitals 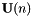 to the new orbitals
to the new orbitals
![\[ \mathbf{U}(n+1) = \mathbf{U}_{add} \mathbf{U}(n) = \exp(\mathbf{X}(\vec{x}(n))) \mathbf{U}(n). \]](form_29.png)
This updating scheme is called the Newton-Raphson method [CAS3]. If the Hessian is positive definite, these updates are stable. For saddle points in the energy landscape, the Hessian has negative eigenvalues, and these updates can be unstable. It is therefore better to use the augmented Hessian Newton-Raphson method [CAS7]:
![\[ \left[ \begin{array}{cc} \mathbf{H} & \vec{g} \\ \vec{g}^T & 0 \end{array} \right] \left[ \begin{array}{c} \vec{x} \\ 1 \end{array} \right] = \alpha \left[ \begin{array}{c} \vec{x} \\ 1 \end{array} \right]. \]](form_30.png)
The eigenvector with smallest algebraic eigenvalue determines a stable update 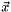 , as is well explained in Ref. [CAS7].
, as is well explained in Ref. [CAS7].
As a final remark in this section, I would like to say that orbitals have gauge freedom. One can always multiply them with a phase factor. It is therefore possible to choose the orbital gauges so that all 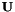 are always special orthogonal:
are always special orthogonal: 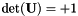 .
.
When the update norm 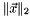 is small enough, the convergence can be accelerated by the direct inversion of the iterative subspace (DIIS) [CAS5, CAS8, CAS9, CAS10]. For a given set of orbitals
is small enough, the convergence can be accelerated by the direct inversion of the iterative subspace (DIIS) [CAS5, CAS8, CAS9, CAS10]. For a given set of orbitals 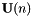 , the update
, the update 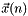 is calculated with the augmented Hessian Newton-Raphson method. This update defines the next set of orbitals:
is calculated with the augmented Hessian Newton-Raphson method. This update defines the next set of orbitals:
![\[ \mathbf{U}(n+1) = \mathbf{U}_{add} \mathbf{U}(n) = \exp(\mathbf{X}(\vec{x}(n))) \mathbf{U}(n). \]](form_29.png)
In DIIS, the error vector 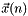 and the state vector
and the state vector 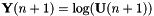 are added to a list. The error
are added to a list. The error
![\[ e = \left\| \sum\limits_{i = 1}^{\kappa} c_i \vec{x}(n - \kappa + i) \right\|_2 \]](form_36.png)
is minimized under the constraint 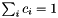 .
. 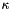 is the size of the list memory, i.e. the number of retained vectors. The minimization of the error
is the size of the list memory, i.e. the number of retained vectors. The minimization of the error 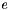 can be performed with Lagrangian calculus:
can be performed with Lagrangian calculus:
![\[ \left[ \begin{array}{cc} \mathbf{B} & \vec{1} \\ \vec{1}^T & 0 \end{array} \right] \left[ \begin{array}{c} \vec{c} \\ \lambda \end{array} \right] = \left[ \begin{array}{c} \vec{0} \\ 1 \end{array} \right], \]](form_40.png)
where 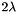 is the Lagrangian multiplier and
is the Lagrangian multiplier and
![\[ \left[\mathbf{B}\right]_{ij} = \vec{x}^T(n - \kappa + i) \vec{x}(n - \kappa + j) = \left[\mathbf{B}\right]_{ji}. \]](form_42.png)
The new state vector is then defined as
![\[ \mathbf{Y}_{new} = \sum\limits_{i = 1}^{\kappa} c_i \mathbf{Y}(n+1 - \kappa + i). \]](form_43.png)
The new state vector 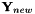 is calculated by the function CheMPS2::DIIS::calculateParam. The current orbitals are then set to
is calculated by the function CheMPS2::DIIS::calculateParam. The current orbitals are then set to 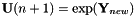 .
.
[CAS1] D. Zgid and M. Nooijen, Journal of Chemical Physics 128, 144115 (2008). http://dx.doi.org/10.1063/1.2883980
[CAS2] D. Ghosh, J. Hachmann, T. Yanai and G.K.-L. Chan, Journal of Chemical Physics 128, 144117 (2008). http://dx.doi.org/10.1063/1.2883976
[CAS3] P.E.M. Siegbahn, J. Almlof, A. Heiberg and B.O. Roos, Journal of Chemical Physics 74, 2384-2396 (1981). http://dx.doi.org/10.1063/1.441359
[CAS4] D. Zgid and M. Nooijen, Journal of Chemical Physics 128, 144116 (2008). http://dx.doi.org/10.1063/1.2883981
[CAS5] T. Yanai, Y. Kurashige, D. Ghosh and G.K.-L. Chan, International Journal of Quantum Chemistry 109, 2178-2190 (2009). http://dx.doi.org/10.1002/qua.22099
[CAS6] S. Wouters, W. Poelmans, P.W. Ayers and D. Van Neck, Computer Physics Communications 185, 1501-1514 (2014). http://dx.doi.org/10.1016/j.cpc.2014.01.019
[CAS7] A. Banerjee, N. Adams, J. Simons and R. Shepard, Journal of Physical Chemistry 89, 52-57 (1985). http://dx.doi.org/10.1021/j100247a015
[CAS8] P. Pulay, Chemical Physics Letters 73, 393-398 (1980). http://dx.doi.org/10.1016/0009-2614(80)80396-4
[CAS9] C.D. Sherrill, Programming DIIS, http://vergil.chemistry.gatech.edu/notes/diis/node3.html (2000).
[CAS10] T. Rohwedder and R. Schneider, Journal of Mathematical Chemistry 49, 1889-1914 (2011). http://dx.doi.org/10.1007/s10910-011-9863-y
| CheMPS2::CASSCF::CASSCF | ( | Hamiltonian * | ham_in, |
| int * | docc, | ||
| int * | socc, | ||
| int * | nocc, | ||
| int * | ndmrg, | ||
| int * | nvirt, | ||
| const string | tmp_folder = CheMPS2::defaultTMPpath |
||
| ) |
Constructor.
| ham_in | Hamiltonian containing the matrix elements of the Hamiltonian for which a CASSCF calculation is desired |
| docc | Array containing the number of doubly occupied HF orbitals per irrep |
| socc | Array containing the number of singly occupied HF orbitals per irrep |
| nocc | Array containing the number of doubly occupied (inactive) orbitals per irrep |
| ndmrg | Array containing the number of active orbitals per irrep |
| nvirt | Array containing the number of virtual (secondary) orbitals per irrep |
| tmp_folder | Temporary work folder for the DMRG renormalized operators and the ERI rotations |
Definition at line 39 of file CASSCF.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:
|
static |
Calculate the augmented Hessian Newton-Raphson update for the orthogonal orbital rotation matrix.
| localFmat | Matrix which contains the Fock operator (Eq. (11) in the Siegbahn paper [CAS3]) |
| localwtilde | Object which contains the second order derivative of the energy with respect to the unitary (Eq. (20b) in the Siegbahn paper [CAS3]) |
| localIdx | Orbital index bookkeeper for the CASSCF calculations |
| localUmat | The unitary matrix for CASSCF calculations (in this function it is used to fetch the orbital ordering convention of the skew-symmetric parametrization) |
| theupdate | Where the augmented Hessian Newton-Raphson update will be stored |
| updateNorm | Pointer to one double to store the update norm |
| gradNorm | Pointer to one double to store the gradient norm |
Definition at line 316 of file CASSCFnewtonraphson.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
static |
Block-diagonalize Mat.
| space | Can be 'O', 'A', or 'V' and denotes which block of Mat should be considered |
| Mat | Matrix to block-diagonalize |
| Umat | The unitary rotation will be updated so that Mat is block-diagonal in the orbitals 'space' |
| work1 | Workspace |
| work2 | Workspace |
| idx | Object which handles the index conventions for CASSCF |
| invert | If true, the eigenvectors are sorted from large to small instead of the other way around |
| two_dm | If not NULL, this 4-index array will be rotated to the new eigenvecs if space == 'A' |
| three_dm | If not NULL, this 6-index array will be rotated to the new eigenvecs if space == 'A' |
| contract | If not NULL, this 6-index array will be rotated to the new eigenvecs if space == 'A' |
Definition at line 433 of file CASSCF.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
static |
Build the F-matrix (Eq. (11) in the Siegbahn paper [CAS3])
| localFmat | Matrix where the result should be stored |
| localTmat | Matrix which contains the one-electron integrals |
| localJKocc | Matrix which contains the Coulomb and exchange interaction due to the frozen core orbitals |
| localJKact | Matrix which contains the Coulomb and exchange interaction due to the active space |
| localIdx | Orbital index bookkeeper for the CASSCF calculations |
| theInts | The rotated two-electron integrals (at most 2 virtual indices) |
| local2DM | The DMRG 2-RDM |
| local1DM | The DMRG 1-RDM |
Definition at line 823 of file CASSCFnewtonraphson.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
static |
Build the Wtilde-matrix (Eq. (20b) in the Siegbahn paper [CAS3])
| localwtilde | Where the result should be stored |
| localTmat | Matrix which contains the one-electron integrals |
| localJKocc | Matrix which contains the Coulomb and exchange interaction due to the frozen core orbitals |
| localJKact | Matrix which contains the Coulomb and exchange interaction due to the active space |
| localIdx | Orbital index bookkeeper for the CASSCF calculations |
| theInts | The rotated two-electron integrals (at most 2 virtual indices) |
| local2DM | The DMRG 2-RDM |
| local1DM | The DMRG 1-RDM |
Definition at line 611 of file CASSCFnewtonraphson.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::CASSCF::caspt2 | ( | const int | Nelectrons, |
| const int | TwoS, | ||
| const int | Irrep, | ||
| ConvergenceScheme * | OptScheme, | ||
| const int | rootNum, | ||
| DMRGSCFoptions * | scf_options, | ||
| const double | IPEA, | ||
| const double | IMAG, | ||
| const bool | PSEUDOCANONICAL, | ||
| const bool | CHECKPOINT = false, |
||
| const bool | CUMULANT = false |
||
| ) |
Calculate the caspt2 correction energy for a converged casscf wavefunction.
| Nelectrons | Total number of electrons in the system: occupied HF orbitals + active space |
| TwoS | Twice the targeted spin |
| Irrep | Desired wave-function irrep |
| OptScheme | The optimization scheme to run the inner DMRG loop. If NULL: use FCI instead of DMRG. |
| rootNum | Denotes the targeted state in state-specific CASSCF; 1 means ground state, 2 first excited state etc. |
| scf_options | Contains the DMRGSCF options |
| IPEA | The CASPT2 IPEA shift from Ghigo, Roos and Malmqvist, Chemical Physics Letters 396, 142-149 (2004) |
| IMAG | The CASPT2 imaginary shift from Forsberg and Malmqvist, Chemical Physics Letters 274, 196-204 (1997) |
| PSEUDOCANONICAL | If true, use the exact DMRG 4-RDM in the pseudocanonical basis. If false, use the cumulant approximated DMRG 4-RDM in the unrotated basis. |
| CHECKPOINT | If true, write checkpoints to disk and read them back in again in order to perform the contraction of the generalized Fock operator with the 4-RDM in multiple runs. |
| CUMULANT | If true, a cumulant approximation is used for the 4-RDM and CHECKPOINT is overwritten to false. If false, the full 4-RDM is used. |
Definition at line 189 of file CASSCFpt2.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:
|
static |
Construct the Fock matrix.
| Fock | Matrix to store the Fock operator in |
| Tmat | Matrix with the one-electron integrals |
| Qocc | Matrix with the Coulomb and exchange contributions of the occupied (inactive) orbitals |
| Qact | Matrix with the Coulomb and exchange contributions of the active space orbitals |
| idx | Object which handles the index conventions for CASSCF |
Definition at line 395 of file CASSCFpt2.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
static |
|
static |
Copy a one-orbital quantity from array format to DMRGSCFmatrix format.
| origin | Array to copy |
| result | DMRGSCFmatrix to store the copy |
| idx | Object which handles the index conventions for CASSCF |
| one_rdm | If true, the occupied orbitals get occupation 2 |
Definition at line 375 of file CASSCF.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
static |
Copy a one-orbital quantity from DMRGSCFmatrix format to array format.
| origin | DMRGSCFmatrix to copy |
| result | Array to store the copy |
| idx | Object which handles the index conventions for CASSCF |
Definition at line 407 of file CASSCF.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:
|
static |
Return the RMS deviation from block-diagonal.
| matrix | Matrix to be assessed |
| idx | Object which handles the index conventions for CASSCF |
Definition at line 411 of file CASSCFpt2.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
static |
From an Edmiston-Ruedenberg active space rotation, fetch the eigenvectors and store them in eigenvecs.
| umat | The Edmiston-Ruedenberg active space rotation |
| idx | Object which handles the index conventions for CASSCF |
| eigenvecs | Where the eigenvectors are stored |
Definition at line 160 of file CASSCF.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
static |
Build the contraction of the fock matrix with the 4-RDM.
| fockmx | Array of size ham->getL() x ham->getL() containing the Fock matrix elements |
| dmrgsolver | DMRG object which is solved, and for which the 2-RDM and 3-RDM have been calculated as well |
| ham | Active space Hamiltonian, which is needed for the size of the active space and the orbital irreps |
| next_orb1 | The next first orbital for which the contraction should be continued |
| next_orb2 | The next second orbital for which the contraction should be continued |
| work | Work array of size ham->getL()**6 |
| result | On entry, contains the partial contraction corresponding to (next_orb1, next_orb2). On exit, contains the full contraction. |
| CHECKPOINT | Whether or not the standard CheMPS2 F.4-RDM checkpoint should be created/updated to continue the contraction at later times |
| PSEUDOCANONICAL | Whether or not pseudocanonical orbitals are used in the active space |
Definition at line 140 of file CASSCFpt2.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| int CheMPS2::CASSCF::get_num_irreps | ( | ) |
|
static |
Read the checkpoint file for the contraction of the generalized Fock operator with the 4-RDM from disk.
| f4rdm_file | The filename |
| hamorb1 | The next hamiltonian orbital 1 |
| hamorb2 | The next hamiltonian orbital 2 |
| tot_dmrg_power6 | The size of the array contract |
| contract | The current partial contraction |
Definition at line 87 of file CASSCFpt2.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
static |
Construct the 1-RDM from the 2-RDM.
| num_elec | The number of DMRG active space electrons |
| LAS | The total number of DMRG orbitals |
| one_dm | The CASSCF 1-RDM |
| two_dm | The CASSCF 2-RDM |
Definition at line 134 of file CASSCF.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::CASSCF::solve | ( | const int | Nelectrons, |
| const int | TwoS, | ||
| const int | Irrep, | ||
| ConvergenceScheme * | OptScheme, | ||
| const int | rootNum, | ||
| DMRGSCFoptions * | scf_options | ||
| ) |
Do the CASSCF cycles with the augmented Hessian Newton-Raphson method.
| Nelectrons | Total number of electrons in the system: occupied HF orbitals + active space |
| TwoS | Twice the targeted spin |
| Irrep | Desired wave-function irrep |
| OptScheme | The optimization scheme to run the inner DMRG loop. If NULL: use FCI instead of DMRG. |
| rootNum | Denotes the targeted state in state-specific CASSCF; 1 means ground state, 2 first excited state etc. |
| scf_options | Contains the DMRGSCF options |
Definition at line 56 of file CASSCFnewtonraphson.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:
|
static |
Write the checkpoint file for the contraction of the generalized Fock operator with the 4-RDM to disk.
| f4rdm_file | The filename |
| hamorb1 | The next hamiltonian orbital 1 |
| hamorb2 | The next hamiltonian orbital 2 |
| tot_dmrg_power6 | The size of the array contract |
| contract | The current partial contraction |
Definition at line 44 of file CASSCFpt2.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function: