 |
CheMPS2
|
 |
CheMPS2
|
#include <Cumulant.h>
Static Public Member Functions | |
| static double | gamma4_ham (const Problem *prob, const ThreeDM *the3DM, const TwoDM *the2DM, const int i, const int j, const int k, const int l, const int p, const int q, const int r, const int s) |
Get the cumulant approximation of 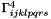 , using HAM indices. More... , using HAM indices. More... | |
| static void | gamma4_fock_contract_ham (const Problem *prob, const ThreeDM *the3DM, const TwoDM *the2DM, double *fock, double *result) |
Contract the CASPT2 Fock operator with the cumulant approximation of 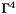 in in 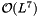 time, using HAM indices. More... time, using HAM indices. More... | |
Cumulant class.
The cumulant class contains routines to approximate the spinfree 4-RDM 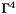 by neglecting the fourth order cumulant
by neglecting the fourth order cumulant 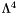 . Based on the spinfree density matrices
. Based on the spinfree density matrices
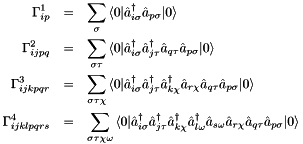
and the spinfree second order cumulant
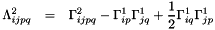
the spinfree 4-RDM can be written as [CUM1]:

By neglecting 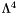 , the cumulant approximation of the 4-RDM
, the cumulant approximation of the 4-RDM 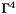 is obtained.
is obtained.
[CUM1] M. Saitow, Y. Kurashige and T. Yanai, Journal of Chemical Physics 139, 044118 (2013). http://dx.doi.org/10.1063/1.4816627
Definition at line 120 of file Cumulant.h.
|
static |
Contract the CASPT2 Fock operator with the cumulant approximation of 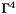 in
in 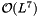 time, using HAM indices.
time, using HAM indices.
| prob | Pointer to the DMRG problem |
| the3DM | Pointer to the DMRG 3-RDM |
| the2DM | Pointer to the DMRG 2-RDM |
| fock | Contains the SYMMETRIC fock operator 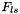 = fock[l+L*s] = fock[s+L*l] = fock[l+L*s] = fock[s+L*l] |
| result | Contains the contraction: result[i+L*(j+L*(k+L*(p+L*(q+L*r))))] = 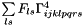 |
Definition at line 84 of file Cumulant.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
static |
Get the cumulant approximation of 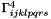 , using HAM indices.
, using HAM indices.
| prob | Pointer to the DMRG problem |
| the3DM | Pointer to the DMRG 3-RDM |
| the2DM | Pointer to the DMRG 2-RDM |
| i | index 1 of 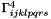 |
| j | index 2 of 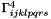 |
| k | index 3 of 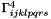 |
| l | index 4 of 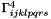 |
| p | index 5 of 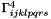 |
| q | index 6 of 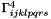 |
| r | index 7 of 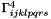 |
| s | index 8 of 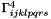 |
Definition at line 381 of file Cumulant.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: