 |
CheMPS2
|
 |
CheMPS2
|
#include <Correlations.h>
Public Member Functions | |
| Correlations (const SyBookkeeper *denBKIn, const Problem *ProbIn, TwoDM *the2DMin) | |
| Constructor. More... | |
| virtual | ~Correlations () |
| Destructor. | |
| double | getCspin_DMRG (const int row, const int col) const |
| Get a Cspin term, using the DMRG indices. More... | |
| double | getCspin_HAM (const int row, const int col) const |
| Get a Cspin term, using the HAM indices. More... | |
| double | getCdens_DMRG (const int row, const int col) const |
| Get a Cdens term, using the DMRG indices. More... | |
| double | getCdens_HAM (const int row, const int col) const |
| Get a Cdens term, using the HAM indices. More... | |
| double | getCspinflip_DMRG (const int row, const int col) const |
| Get a Cspinflip term, using the DMRG indices. More... | |
| double | getCspinflip_HAM (const int row, const int col) const |
| Get a Cspinflip term, using the HAM indices. More... | |
| double | getCdirad_DMRG (const int row, const int col) const |
| Get a Cdirad term, using the DMRG indices. More... | |
| double | getCdirad_HAM (const int row, const int col) const |
| Get a Cdirad term, using the HAM indices. More... | |
| double | getMutualInformation_DMRG (const int row, const int col) const |
| Get a mutual information term, using the DMRG indices. More... | |
| double | getMutualInformation_HAM (const int row, const int col) const |
| Get a mutual information term, using the HAM indices. More... | |
| double | SingleOrbitalEntropy_DMRG (const int index) const |
| Get the single-orbital entropy for a certain site, using the DMRG indices. More... | |
| double | SingleOrbitalEntropy_HAM (const int index) const |
| Get the single-orbital entropy for a certain site, using hte HAM indices. More... | |
| void | FillSite (TensorT *denT, TensorGYZ **Gtensors, TensorGYZ **Ytensors, TensorGYZ **Ztensors, TensorKM **Ktensors, TensorKM **Mtensors) |
| Fill at the current step of the iterations the two-orbital mutual information and the remaining part of Cdirad. More... | |
| double | MutualInformationDistance (const double power) const |
| Return Idistance(power) (see return for definition) More... | |
| void | Print (const int precision=6, const int columnsPerLine=8) const |
| Print the correlation functions and two-orbital mutual information. More... | |
| void | mpi_broadcast () |
| Broadcast the diradical correlation function and the two-orbital mutual information. | |
Correlations class.
Orbital correlation can be quantified by means of the two-orbital mutual information, as well as several correlation functions. The two-orbital mutual information was introduced in quantum chemistry by Rissler [COR1] in order to find the optimal orbital ordering for DMRG calculations. Later, the groups of Legeza and Reiher used this quantum information measure to study both the orbital ordering, as well as the molecular electronic structure [COR2, COR3, COR4, COR5]. The two-orbital mutual information can be interpreted in terms of generalized correlation functions, which reveal the detailed nature of the electron correlation [COR6].
In quantum chemistry, molecular electronic structure is often interpreted in terms of single-particle states, called orbitals. For correlated calculations, the orbital occupations become entangled, which is in contrast to Hartree-Fock theory, where the orbitals have definite occupations. Several measures from quantum information theory allow to quantify orbital correlation. From the total Hilbert space, a subset 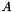 of orbitals can be selected. Denote by
of orbitals can be selected. Denote by 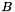 the complement of
the complement of 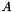 , i.e. the other orbitals which form together with
, i.e. the other orbitals which form together with 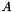 the total Hilbert space. From a wavefunction in the total Hilbert space
the total Hilbert space. From a wavefunction in the total Hilbert space 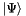 , the (positive semidefinite) reduced density matrix of
, the (positive semidefinite) reduced density matrix of 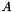 can be calculated as
can be calculated as
![\[ \mathbf{\rho}_A = trace_{B} ~ \ket{\Psi}\bra{\Psi}, \]](form_52.png)
where 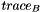 denotes the summation over the occupations of the orbitals in
denotes the summation over the occupations of the orbitals in 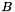 . The (nonnegative) eigenspectrum of
. The (nonnegative) eigenspectrum of 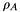 directly reflects the quantum entanglement between the orbitals in
directly reflects the quantum entanglement between the orbitals in 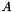 and the ones in
and the ones in 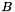 . If there is only one nonzero eigenvalue,
. If there is only one nonzero eigenvalue, 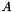 and
and 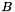 are not entangled. The total wavefunction can then be factorized:
are not entangled. The total wavefunction can then be factorized: 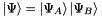 . A measurement of an occupation in
. A measurement of an occupation in 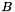 does not influence the outcome of a measurement in
does not influence the outcome of a measurement in 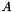 . If there are several nonzero eigenvalues,
. If there are several nonzero eigenvalues, 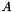 and
and 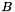 are entangled, and measurements in
are entangled, and measurements in 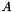 and
and 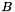 are correlated. The total wavefunction can not be factorized in that case.
are correlated. The total wavefunction can not be factorized in that case.
The von Neumann entropy is a measure which quantifies the amount of entanglement between 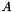 and
and 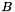 :
:
![\[ S_{A \mid B} = -trace_A ~ \mathbf{\rho}_A \log( \mathbf{\rho}_A ) = S_{B \mid A} \geq 0. \]](form_56.png)
If 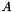 and
and 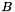 are unentangled,
are unentangled, 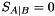 . With increasing entanglement between
. With increasing entanglement between 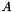 and
and 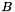 ,
, 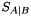 becomes larger. When
becomes larger. When 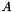 consists of a single orbital
consists of a single orbital 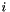 , the von Neumann entropy is called the single-orbital entropy
, the von Neumann entropy is called the single-orbital entropy 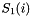 . When
. When 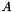 consists of two orbitals
consists of two orbitals 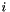 and
and 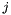 , the von Neumann entropy is called the two-orbital entropy
, the von Neumann entropy is called the two-orbital entropy 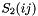 . The following inequality holds between them:
. The following inequality holds between them:
![\[ S_2(ij) \leq S_1(i) + S_1(j), \]](form_63.png)
the so-called subadditivity property. Any entanglement between orbitals 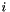 and
and 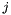 reduces
reduces 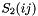 with respect to
with respect to 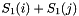 . The amount of entanglement between two orbitals can then be quantified by means of the two-orbital mutual information
. The amount of entanglement between two orbitals can then be quantified by means of the two-orbital mutual information
![\[ \left[ \mathbf{I} \right]_{ij} = \frac{1}{2} \left( S_1(i) + S_1(j) - S_2(ij) \right) \left( 1 - \delta_{ij} \right) = \left[ \mathbf{I} \right]_{ji} \geq 0. \]](form_65.png)
With increasing entanglement between orbitals 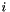 and
and 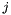 ,
, ![$\left[ \mathbf{I} \right]_{ij}$](form_66.png) becomes larger. In DMRG, this measure can be calculated efficiently [COR1, COR5, COR6]. In a spin-adapted DMRG code, there are only 16 unique elements instead of the 26 which are described in Ref. [COR5].
becomes larger. In DMRG, this measure can be calculated efficiently [COR1, COR5, COR6]. In a spin-adapted DMRG code, there are only 16 unique elements instead of the 26 which are described in Ref. [COR5].
In addition to the two-orbital mutual information, CheMPS2 also provides access to four other correlation functions. Three of them can be obtained from the reduced 2-RDMs 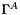 and
and 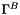 , and from the reduced 1-RDM
, and from the reduced 1-RDM 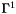 :
:
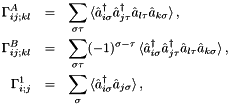
where 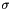 and
and 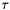 can be
can be 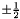 . These correlation functions are the spin correlation function
. These correlation functions are the spin correlation function
![\[ C_{spin}(i,j) = 4 \left( \braket{\hat{S}_i^z \hat{S}_j^z} - \braket{\hat{S}_i^z} \braket{\hat{S}_j^z} \right) = \Gamma^B_{ij;ij} + \delta_{ij} \Gamma^1_{i;i}, \]](form_74.png)
(where 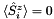 due to the spin-adaptation), the spin-flip correlation function
due to the spin-adaptation), the spin-flip correlation function
![\[ C_{spinflip}(i,j) = \braket{\hat{S}_i^+ \hat{S}_j^-} + \braket{\hat{S}_i^- \hat{S}_j^+} = \frac{1}{2} \left( \Gamma^B_{ij;ji} - \Gamma^A_{ij;ji} \right) + \delta_{ij} \Gamma^1_{i;i}, \]](form_76.png)
and the density correlation function
![\[ C_{dens}(i,j) = \braket{\hat{n}_i \hat{n}_j} - \braket{\hat{n}_i} \braket{\hat{n}_j} = \Gamma^A_{ij;ij} + \Gamma^1_{i;i} \left( \delta_{ij} - \Gamma^1_{j;j} \right). \]](form_77.png)
The fourth one is the singlet diradical correlation function [COR7]
![\[ C_{dirad}(i,j) = \braket{\hat{d}_{i\uparrow} \hat{d}_{j\downarrow}} + \braket{\hat{d}_{i\downarrow} \hat{d}_{j\uparrow}} - \braket{\hat{d}_{i\uparrow}} \braket{\hat{d}_{j\downarrow}} - \braket{\hat{d}_{i\downarrow}} \braket{\hat{d}_{j\uparrow}}, \]](form_78.png)
where 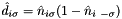 .
.
The two-orbital mutual information and these correlation functions are calculated in the function CheMPS2::DMRG::calc2DMandCorrelations.
[COR1] J. Rissler, R. M. Noack and S.R. White, Chemical Physics 323, 519-531 (2006). http://dx.doi.org/10.1016/j.chemphys.2005.10.018
[COR2] G. Barcza, O. Legeza, K.H. Marti, M. Reiher, Physical Review A 83, 012508 (2011). http://dx.doi.org/10.1103/PhysRevA.83.012508
[COR3] K. Boguslawski, K.H. Marti, O. Legeza and M. Reiher, Journal of Chemical Theory and Computation 8, 1970-1982 (2012). http://dx.doi.org/10.1021/ct300211j
[COR4] K. Boguslawski, P. Tecmer, O. Legeza and M. Reiher, Journal of Physical Chemistry Letters 3, 3129-3135 (2012). http://dx.doi.org/10.1021/jz301319v
[COR5] K. Boguslawski, P. Tecmer, G. Barcza, O. Legeza and M. Reiher, Journal of Chemical Theory and Computation 9, 2959-2973 (2013). http://dx.doi.org/10.1021/ct400247p
[COR6] G. Barcza, R.M. Noack, J. Solyom, O. Legeza, http://arxiv.org/abs/1406.6643 (2014).
[COR7] J. Hachmann, J.J. Dorando, M. Aviles and G.K.-L. Chan, Journal of Chemical Physics 127, 134309 (2007). http://dx.doi.org/10.1063/1.2768362
Definition at line 98 of file Correlations.h.
| CheMPS2::Correlations::Correlations | ( | const SyBookkeeper * | denBKIn, |
| const Problem * | ProbIn, | ||
| TwoDM * | the2DMin | ||
| ) |
Constructor.
| denBKIn | Symmetry sector bookkeeper |
| ProbIn | The problem to be solved |
| the2DMin | The 2-RDM of the active space |
Definition at line 35 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:| void CheMPS2::Correlations::FillSite | ( | TensorT * | denT, |
| TensorGYZ ** | Gtensors, | ||
| TensorGYZ ** | Ytensors, | ||
| TensorGYZ ** | Ztensors, | ||
| TensorKM ** | Ktensors, | ||
| TensorKM ** | Mtensors | ||
| ) |
Fill at the current step of the iterations the two-orbital mutual information and the remaining part of Cdirad.
| denT | DMRG site-matrices |
| Gtensors | Tensors required for the calculation |
| Ytensors | Tensors required for the calculation |
| Ztensors | Tensors required for the calculation |
| Ktensors | Tensors required for the calculation |
| Mtensors | Tensors required for the calculation |
Definition at line 212 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::Correlations::getCdens_DMRG | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a Cdens term, using the DMRG indices.
| row | the first index |
| col | the second index |
Definition at line 117 of file Correlations.cpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::Correlations::getCdens_HAM | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a Cdens term, using the HAM indices.
| row | the first index |
| col | the second index |
Definition at line 119 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:| double CheMPS2::Correlations::getCdirad_DMRG | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a Cdirad term, using the DMRG indices.
| row | the first index |
| col | the second index |
Definition at line 141 of file Correlations.cpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::Correlations::getCdirad_HAM | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a Cdirad term, using the HAM indices.
| row | the first index |
| col | the second index |
Definition at line 143 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:| double CheMPS2::Correlations::getCspin_DMRG | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a Cspin term, using the DMRG indices.
| row | the first index |
| col | the second index |
Definition at line 105 of file Correlations.cpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::Correlations::getCspin_HAM | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a Cspin term, using the HAM indices.
| row | the first index |
| col | the second index |
Definition at line 107 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:| double CheMPS2::Correlations::getCspinflip_DMRG | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a Cspinflip term, using the DMRG indices.
| row | the first index |
| col | the second index |
Definition at line 129 of file Correlations.cpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::Correlations::getCspinflip_HAM | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a Cspinflip term, using the HAM indices.
| row | the first index |
| col | the second index |
Definition at line 131 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:| double CheMPS2::Correlations::getMutualInformation_DMRG | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a mutual information term, using the DMRG indices.
| row | the first index |
| col | the second index |
Definition at line 153 of file Correlations.cpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::Correlations::getMutualInformation_HAM | ( | const int | row, |
| const int | col | ||
| ) | const |
Get a mutual information term, using the HAM indices.
| row | the first index |
| col | the second index |
Definition at line 155 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function:| double CheMPS2::Correlations::MutualInformationDistance | ( | const double | power | ) | const |
Return Idistance(power) (see return for definition)
| power | The power used in Idistance |
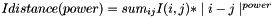
Definition at line 188 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| void CheMPS2::Correlations::Print | ( | const int | precision = 6, |
| const int | columnsPerLine = 8 |
||
| ) | const |
Print the correlation functions and two-orbital mutual information.
| precision | The number of digits to be printed |
| columnsPerLine | Rarara: The number of columns per line |
Definition at line 602 of file Correlations.cpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::Correlations::SingleOrbitalEntropy_DMRG | ( | const int | index | ) | const |
Get the single-orbital entropy for a certain site, using the DMRG indices.
| index | The DMRG index |
Definition at line 165 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| double CheMPS2::Correlations::SingleOrbitalEntropy_HAM | ( | const int | index | ) | const |
Get the single-orbital entropy for a certain site, using hte HAM indices.
| index | The HAM index |
Definition at line 179 of file Correlations.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function: